My Program

切換瀏覽器標頭-User Agent Switcher

這個是一個 Firefox 的插件, 叫做 User Agent Switcher

現在開發手機上應用的網頁機會比以往多, 但是礙於測試時期, 一般這些網頁程式都會檢查使用者的瀏覽器(User Agent), 所以使用這個插件, 方便使用者在切換自己的瀏覽器的標頭.

安裝好之後, 會在[工具]功能表內, 多出一個切換 User Agent 的功能, 如下所示:

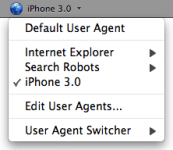
(圖片引用自: https://addons.mozilla.org/zh-TW/firefox/addon/59)

如此一來, 便能方便測試網頁程式, 對於不同的 User Agent 的判定, 及行為驗證, 將會有很大的幫助, 而不需要準備太多環境. 當然, 若是要做所謂的 HTML, CSS, JAVASCRIPT 相容性測試, 則這個就比較幫不上忙了, 但對於判定 User Agent 而要重導使用者, 或產生一些不同的功能時, 可以很快速的驗證.

像是 naver.jp 這個網站, 有個 for iphone 的版本 (http://ipn.naver.jp) , 會檢查User Agent來重導使用者到 http://www.naver.jp, 就沒辦法預覽到 iphone 的頁面了. 使用這個 User Agent Switcher 時, 就能”假裝” Firefox 是 iphone 的 browser , 來訪問該網頁囉!

[2010/6/15 0:05]
補充一下相關的 user agent 資料, 可以利用匯入的方式達成, 請如以下操作:
1. Default User Agent, Edit User Agents:

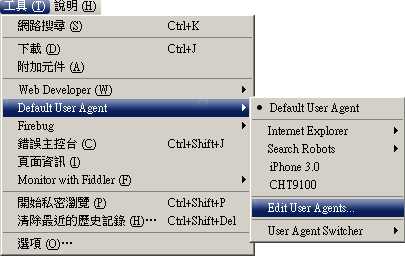
2. 在畫面上選擇下方的 Import:

3. 到這裡下載已整理好的 user agent xml 檔: http://techpatterns.com/forums/about304.html
(或直接對這個連結按右鍵另存新檔: http://techpatterns.com/downloads/firefox/useragentswitcher.xml)
4. 於 import 選擇剛下載的檔案即可, 在 User Agent Switcher 就會有很多的 user agent 出來了, 還包含 iPad 耶!

PS. 請注意只是切換 User Agent 來讓 web server 吐出對應的 html, 並非是將 firefox 模擬出該 user agent 的呈現效果!!

標籤 extension, Firefox, iphone, plugin, user-agent

好用軟體

使用WebSitePulse檢查網站

這個網站工具 WebSitePulse (http://www.websitepulse.com/) 是用來檢查從世界各地的端點看你的網站是否連線順利正常. 而其中又有從中國大陸的點來做檢查, 就可以知道是否被 GFW 封鎖了.

從介面上選擇 [Free Tools][Web Tools][Website][China Firewall Test] 如下圖:

就可以從外點進行測試囉, 還蠻方便好用的呢!

而中國大陸的測試點有:

Shanghai, China
Beijing, China
Guangzhou, China
Hong Kong, China

方便進行測試比較, 而且也可以同時選擇非中國大陸的地點做對照測試, 可以加強測試的結果比較. 另外也有許多其他方便從外點測試的工具可以用, 方便從不同的網路環境來進行測試並了解網站的狀況.

參考資料: http://www.techbang.com.tw/?p=30460

標籤 GFW, websitepulse

.net

利用ashx傳送檔案下載

在 asp.net 中, 若要實現檔案下載處理的方式(並且要進行 url 隱藏及下載管理), 可以利用 ashx (generic handler) 來進行, 方式很單純, 主要是在 header 上下一些手腳, 方式如下:

<%@ WebHandler Language="C#" Class="file" %>

using System;
using System.Web;

public class file : IHttpHandler {
    
    public void ProcessRequest (HttpContext context) {
        //context.Response.ContentType = "text/plain";
        //context.Response.Write("Hello World");
        //context.Response.ContentType = "image/png";
        //context.Response.TransmitFile("images/m2.png");        
        context.Response.ContentType = "application/octet-stream";
        context.Response.AppendHeader("Content-Disposition", "attachment; filename=test.doc");
        context.Response.TransmitFile("files/test.doc");        
        
    }
 
    public bool IsReusable {
        get {
            return false;
        }
    }

}

使用的方式若是處理檔案下載, 可以利用 application/octet-stream 這個 ContentType header , 並配合 Content-Disposition header 中, 利用 attachment; filename=xxxx 的方式來將檔案名稱指定給客戶端, 參考資料: http://support.microsoft.com/?scid=kb%3Ben-us%3B260519

而之後再利用 TransmitFile() 方法, 將在 server 上的檔案讀取出來並傳送到客戶端, 至於使用 TransmitFile 方法和其他方法的比較如這篇文章所示: http://blog.miniasp.com/post/2008/03/Caution-about-ASPNET-Response-a-Large-File.aspx

一般來說, 若是大檔案, 可以直接利用 TransmitFile 的方式來進行, 但不是太大型檔案, 有續傳需求時, 則不適用, 但效率上是以 TransmitFile 的效率最佳(因為不用先整個讀到記憶體中).

其他人的比較資料:
[ASP.NET] 無網址的檔案下載 – 進階研究 http://gogo1119.pixnet.net/blog/post/27407222

[2010/2/12 14:48]
相關文章: http://edu.uuu.com.tw/data_article/article/100212tips.htm

標籤 ashx, ASP.NET, download, file

瀏覽器的戰火延燒到顯示卡了

最後, 很多服務都需要瀏覽器, 但是在這之前, FLASH10 的 Adobe 宣佈支援顯示卡處理器 (GPU) (link), IE9 的微軟也宣佈要利用 Direct2D, DocumentWrite 來加速及強化顯示效能 (link), 而 Firefox 更是快速地發表了 Firefox 3.7 Alpha版本支援 Direct2D GPU 技術的版本 (link), 預計明年春天正式版發表, 看來, 瀏覽器的戰火延燒到了顯示效率這裡來了.

其實這也是很正常的事, 因為瀏覽器的確需要跑的內容愈來愈華麗, 也愈來愈多層, 耗掉的系統資源也就愈來愈重了, 之前像是一些影音壓縮/解壓縮的程式, 也有支援 GPU 的版本, 讓效率更好, 佔用較少的系統資料, 而改用顯示卡的計算能力來加強影音壓縮和解壓縮的功能.

而現在, 針對瀏覽器強化顯示而使用的 Direct2D 也讓瀏覽器在顯示時, 發揮顯示卡的 GPU 功能, 把效率更提升, 這樣的設計很棒, 把應該發揮的功能發揮出來. 看一下效率測試資料囉:

(圖片引用自: http://www.techbang.com.tw/?p=28019 )

這樣看起來, 應該是原本比較文字的內容有強化到, 而原本不是文字的網頁則沒有差異太多, 無論如何, 對於實際應用應該都會有幫助, 期待 IE9, FX3.7 的正式版本來臨.

標籤 Direct2D, Firefox, GPU, IE

系統技術

免費SSL申請憑證-StartSSL

在寫作 web application 後, 最後一步就是部署發行了.

不過這端往往會有問題(其實也不是問題)的地方在於自己的網站, 若是要使用 SSL 加密通道, 走 https 通訊協議時, 會需要申請一個 SSL 的憑證.

今天剛好在這裡看到一篇文章: http://blog.s135.com/startssl/ 裡有提到有關免費申請的 SSL 憑證. 這家公司是 startcom, 其網站在: http://www.startssl.com , 提供了線上免費申請 SSL 的憑證, 十分方便而且實用.

其實 SSL 憑證是可以自己簽發的, 在自家網路內部還不成問題, 可以將 CA 加入在公司內的電腦主機上, 但是在公眾網路上, 若是瀏覽器沒有內建的 CA 時, 就會發生不信任警告, 而現在的瀏覽器更是主動直接拒絕連結, 需要使用者自行手動加入信任才行. 對於一般的應用上, 自行簽發的憑證真的不是很方便(雖然一樣可以用, 只是信任度就下降了, 不然何必要第三方公證單位的CA呢). 而一般的申請單位像是 Verisign 也都可以申請, 只是費用就不是市井小民負擔的起的.

好. 廢話不多說, 我們就來申請試看看吧, 首先上 http://www.startssl.com 進行申請, 首先到右上有個門有鑰匙的符號進行申請, 之後出現三個功能, Authenticaion, Sign-up, express line, 時選擇 Sign-up, 填入基本資料後, 就可以利用 email 完成驗證身份的動作了.

接下來就可以在 control panel 上的 Validations Wizard 進行 web ssl 憑證申請囉, 畫面如下:

閱讀全文

標籤 Certificate, https, SSL, startcom, startssl

程式技術

GO語言

文章作者作者: tim
文章發佈日期 2009-11-13
在〈GO語言〉中尚無留言

不要吧…

已經一堆學不完的程式語言, GOOGLE又來做這個很妙的超大型計劃, GOLang, 詳情可以參考新聞: http://www.zdnet.com.tw/news/web/0,2000085679,20142689,00.htm

其實我並不覺得這麼多的程式語言有什麼好, 基本上, 所有的程式語言都大同小異, (雖然有的還是有很大的差異), 不過無論如何, 每種語言有每種語言的強項, 也有弱項, 只是一直出新的, 不好好維護舊的, 大打”商品行銷”戰, 到底是為了什麼, 要忙死我們程式設計人員嗎?

不過本著學習是 Developer 最重要的興趣, 我們還是來看看 Golang 在賣什麼, 先到官方網站來看看: http://golang.org/ 網頁真是很有 google 的感覺, 簡潔.

然後 go 語言看起來又像是 C++, 又像是 Java, 也像 script 的 php, 可能都不會差太多吧.

好吧, 只好之後再花一些時間來研究看囉, 這個 google 創建的新語言, go….

標籤 go, Google

Database

SQL Server Replication示意圖

SQL Server Replication (複寫), 也就是用來做資料庫內容同步的一種應用架構, 通常用來做備援或查詢主機應用, 剛在 MSDN 上看到一張說明的圖示很棒, 引用過來, 方便想了解 Replication 技術的朋友參考:

圖片引用自: http://msdn.microsoft.com/en-us/library/aa179423(SQL.80).aspx

其中很重要的觀念在於 snapshot 是做整個資料的複寫, 而 log reader 則是把 transcation log 讀出來存入 distribution database , 再對 subscriber 寫入, 而存在 distribution database 中的 transaction log 用來做資料同步後的持續異動記錄, 以繼續同步 subscriber 中的資料. 由這張圖上看就清楚很多了.

標籤 log reader, Replication, snapshot, SQL Server

懶得分類

下方購物廣告的系統轉換由monday轉為yahoo(批次作業)

先說明一下, 這篇純綷只是一個工商文. 不過也是小站的廣告, 所以請大家將就一下.

話說最近 yahoo 發 email 通知, 即將停止興奇大聯盟的服務, 而需要大家來進行系統轉換(其實不是系統轉換, 而是重新加入 yahoo 大聯盟的服務). 比較麻煩的是沒有那種一次就可以轉換過去的方式, 因為原本就上了一堆廣告產品, 但是有方法, 而且還蠻單純的.

其實早在去年底, 興奇購物就已被 yahoo 購物併購了, 只是系統轉換和介接需要時間, 現在進行系統調整其實也理所當然, 所以只能配合調整, 不過其實這個 yahoo 購物和興奇購物的內容目前是完全一樣的.

所以, 有在用的大家, 就去 yahoo 大聯盟註冊一下, 然後用著一模一樣的後台操作, 挑選一下商品, 並取得代碼如下:

再看看原本的興奇大聯盟的代碼:

其實就只有紅色和綠色字的不同而已, 所以基本上, 可以利用文字編輯器, 如 emeditor, ultraeditor 等將網頁上的廣告 replace 這些文字即可,

1. 為由 partner.monday.com.tw 換為 partner.buy.yahoo.com.tw
2. 由 mcode=MbbbPQ== 換為 mcode=MaaaPQ==

其中 MbbbPQ== 是你在 monday 的舊代碼(實際沒這麼短, 我是調整一下方便說明), 而 MaaaPQ== 是你在 yahoo 的新代碼, 所以總共只要 replace 2次即可完成新舊版轉換, 但重點是你要先去 yahoo 大聯盟加入, 並新生成一個廣告, 才能取得那個新的 mcode . 若有任何問題, 請與官方聯絡, 這裡只是提供一個轉換的小捷徑而已. 也還請大家多多利用下方的購物連結, 沒買看看也好.

標籤 monday, yahoo

google docs的方程式編輯器

稍早看到這篇新聞: http://www.zdnet.com.tw/news/web/0,2000085679,20141517,00.htm , 其中我比較感興趣的是有關方程式編輯器的功能(equation editor).

google 的這個在 docs 中的 equation editor 是基於 LaTex 的語法實作出來的方程式編輯器, 所以基本上可以參考這裡的資料, 了解一下什麼是 LaTex : http://en.wikipedia.org/wiki/LaTeX , 簡單地說, 就把它想成一個 format script 或是 tag 來展現方程式語法. 上面是一個”平方和”的公式, 利用 equation editor 在 google docs 中的方程式編輯好, 還可以轉貼出來, 這是在寫上一篇文章時發現的功能, 例如上面的方程式:

$\sum_{i=1}^{n}{i^2} =\frac{n(n+1)(2n+1)}{6}$

他的語法為: \sum_{i=1}^{n}{i^2} =\frac{n(n+1)(2n+1)}{6}
圖檔連結為: http://chart.apis.google.com/chart?cht=tx&chs=1×0&chf=bg,s,FFFFFF00&chco=000000&chl=%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%7Bi%5E2%7D%20%3D%5Cfrac%7Bn%28n%2B1%29%282n%2B1%29%7D%7B6%7D

其實也就是利用 google charts api 的引擎, 加入 LaTex 的繪製功能, 把 equation 繪製出來這樣. 但 google 應該是沒有開放這樣的功能供外連, 根據 google charts api 連結: http://code.google.com/intl/zh-TW/apis/chart/ , 並沒有 LaTex equation 的功能, 不過有需要用到的, 可以這樣利用.

利用這個功能實際寫作的文章是這篇: https://diary.tw/archives/896 (數學證明題-平方和), 畢竟用冷冷的文字來說明數學式, 還不如用方程式來展現說明來得清楚, 若是能好好利用的話, 在應用上將會有很大的便利. 尤其是又和 LaTex 相容, 這個真是方便又好用咧!

繼續閱讀:
http://googlesystem.blogspot.com/2009/09/google-docs-has-equation-editor.html

其他的 equation editor:
http://www.codecogs.com/components/equationeditor/equationeditor.php
http://www.sitmo.com/latex/

標籤 docs, equation, Google, LaTex

數學

數學證明題-平方和

文章作者作者: tim
文章發佈日期 2009-09-29
在〈數學證明題-平方和〉中尚無留言

還記得高中有學過證明累加的公式算法嗎? 利用數學歸納法來證明公式是否正確的一個方法, 為了再次熟悉以前的數學, 整理一下數學歸納法的方式.

先來看看 wikipedia 上的定義吧: http://zh.wikipedia.org/zh-tw/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95

利用數學歸納法, 可以證明數學問題的公式, 例如我們要證明平方和這個公式為 n(n+1)(2n+1)/6 於是就利用如下的步驟:

當 n = 1 時, 1^2 = 1, 1 * (1+1) * (2 * 1 + 1) / 6 = 1 成立
假設 n = m 時, 1^2 + 2^2 + 3^2 + … + m^2 = m(m+1)(2m+1)/6 成立
則 n = m+1 時, 應該就是 m(m+1)(2m+1)/6 + (m+1)^2 (也就是 2式 + (m+1)^2), 展開後得: (2m^3+9m^2+13m+6)/6
利用 n=m+1 的公式解得 (m+1)((m+1)+1)(2*(m+1)+1)/6 展開得: (m+1)(m+2)(2m+3)/6 = (2m^3+9m^2+13m+6)/6 和 3. 式結果相同
故得證.

不過用這種不是數學式的寫法看起來不是很舒服, 利用 google docs 的 “公式編輯器” 來寫應該更清楚, 如下:

證明平方和公式為:
$\sum_{i=1}^{n}{i^2} =\frac{n(n+1)(2n+1)}{6}$ 1. 當 n = 1 時, $\sum_{i=1}^{1}{i^2} =\frac{1(1+1)(2\times1+1)}{6} = \frac{1\times2\times3}{6}=1$ 成立

2. 假設 n = m 時, $\sum_{i=1}^{m}{i^2} =\frac{m(m+1)(2m+1)}{6}$ 成立

3. 則當 n = m + 1 時, $\sum_{i=1}^{m+1}{i^2} =\sum_{i=1}^{m}{i^2} + (m+1)^2 = \frac{m(m+1)(2m+1)}{6} + (m+1)^2 = \frac{(2m^3 +9m^2+13m+6)}{6}$ 4. 利用 n = m+1 的公式展開得:

$\sum_{i=1}^{m+1}{i^2} =\frac{(m+1)((m+1)+1)(2(m+1)+1)}{6}=\frac{(2m^3 +9m^2+13m+6)}{6}$

5. 3和4式結果相同, 故得證.

相信這個證明很清楚地證明了平方和的公式及驗證, 也是數學歸納法的證明方式, 是不是讓久未碰高中數學的各位, 喚起了一些些記憶呢?

標籤 mathematics

2025 年 9 月
日	一	二	三	四	五	六
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30