標籤: mathematics

分類
好用軟體

方便好用的線上函數繪圖-graphr.org

這個網站(http://graphr.org/)利用了 html5 的 canvas 特性, 製作了一個方便的函數繪圖功能, 也將一些常用的尋解功能放在上面, 例如二元一次方程式如下:

y=x-1
y=3x-4

把資料輸入後(預設只有一個方程式, 按下[Evaluate]旁的[+]可以再多添加一個方程式), 點 [Evaluate] 後, 會把函數圖繪製出來, 再按下 [Intersect] 鈕, 把滑鼠移到交叉點附近後, 就會出現交點的解, 如下圖:

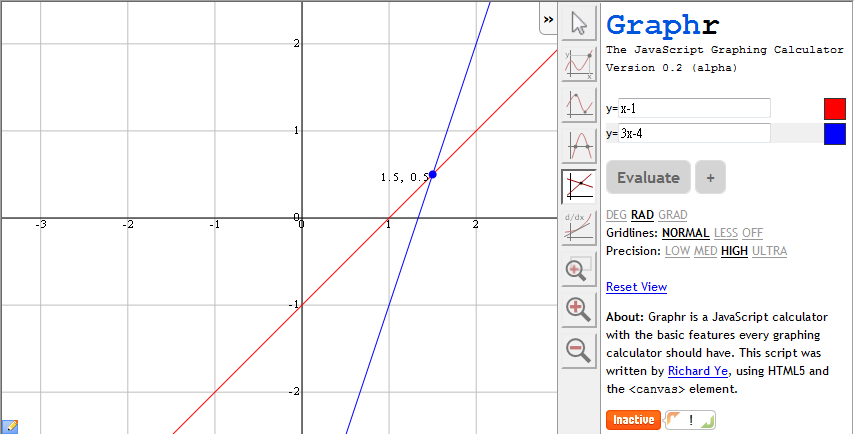
如此一來便能方便地利用圖示函數應用來解一些方程式. 上圖找出 (x, y)=(1.5, 0.5)為解.

再來看看3次函數的局部最大/最小值, 例如以下三次方程式:

y=x^3-3x^2+2

一樣的方式先輸入後, 按下 [Evaluate] 繪出圖形後, 再利用 [Local Minima/Maxima] 鈕, 找局部最大/最小值, 如下圖:

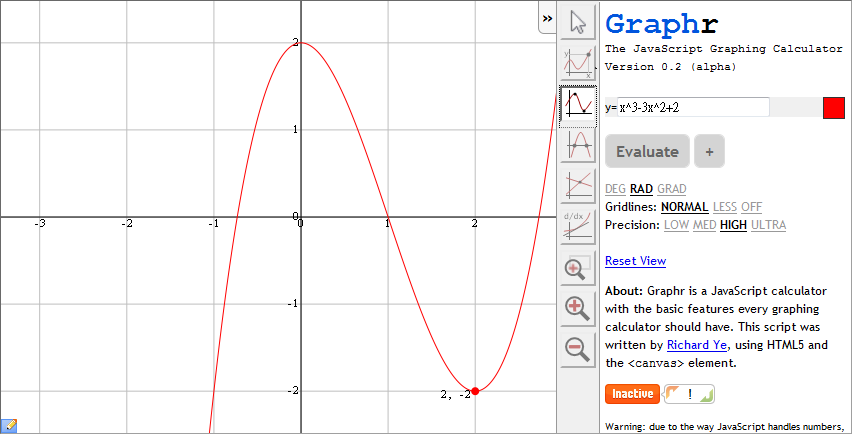
上圖找出 x=2, y=-2 的局部極小值.

很方便的函數繪圖工具.

分類
數學

數學證明題-平方和

還記得高中有學過證明累加的公式算法嗎? 利用數學歸納法來證明公式是否正確的一個方法, 為了再次熟悉以前的數學, 整理一下數學歸納法的方式.

先來看看 wikipedia 上的定義吧: http://zh.wikipedia.org/zh-tw/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95

利用數學歸納法, 可以證明數學問題的公式, 例如我們要證明平方和這個公式為 n(n+1)(2n+1)/6 於是就利用如下的步驟:

  1. 當 n = 1 時, 1^2 = 1, 1 * (1+1) * (2 * 1 + 1) / 6 = 1 成立
  2. 假設 n = m 時, 1^2 + 2^2 + 3^2 + … + m^2 = m(m+1)(2m+1)/6 成立
  3. 則 n = m+1 時, 應該就是 m(m+1)(2m+1)/6 + (m+1)^2 (也就是 2式 + (m+1)^2), 展開後得: (2m^3+9m^2+13m+6)/6
  4. 利用 n=m+1 的公式解得 (m+1)((m+1)+1)(2*(m+1)+1)/6 展開得: (m+1)(m+2)(2m+3)/6 = (2m^3+9m^2+13m+6)/6 和 3. 式結果相同
  5. 故得證.

不過用這種不是數學式的寫法看起來不是很舒服, 利用 google docs 的 “公式編輯器” 來寫應該更清楚, 如下:

證明平方和公式為:
1. 當 n = 1 時, 成立

2. 假設 n = m 時, 成立

3. 則當 n = m + 1 時, 4. 利用 n = m+1 的公式展開得:

5. 3和4式結果相同, 故得證.

相信這個證明很清楚地證明了平方和的公式及驗證, 也是數學歸納法的證明方式, 是不是讓久未碰高中數學的各位, 喚起了一些些記憶呢?

分類
懶得分類

不過就是寫程式嘛

寫程式到底需不需要懂數學？

筆者曾在幾年前和網友討論過有關這類問題. 恰巧今天在 Mr. & Ms. Days 那裡看到這篇: 寫程式到底需不需要懂數學？ 其實正反兩方應該都可以舉出不少實例及說法來證實這些論點.

寫程式需要好的邏輯及理解能力, 至於是否需不需要懂數學, 並非一定, 但大多數的狀況是有絕的幫助, 數學會增進你的推理邏輯能力, 能有效提昇程式的品質, 但不見得程式寫得好的人數學就好, 這個應該是一個比較普遍的概念.

我之前討論狀況是為了鼓勵網友, 有興趣寫程式, 不需要一定會數學, 但邏輯能力一定要好, 不然很難寫出有條理的 code. 若不是在做數理底層或壓縮或演算法, 其實數學只需要基本概念即可, 畢竟大多數的演算法, 壓縮器等都有現成的 library, 寫一般的程式, 應該都用不太到自己實作這些東西, 反倒是如何應用, 或知道這些用法是比較重要的.

軟體IC在談的就是這個概念, 如何重用, 有效組合, 將程式實作發揮戰力, 這才是最重要的, 但多了解, 多學習, 有好的數學基礎, 好的邏輯基礎, 程式應用的 domain know-how 更能加分.

看到了 Mr. & Ms. Days 其中一張圖很感慨, 因為往往程式專案都會發生這樣類似的狀況, 但如何能更有效解決, 我想這應該需要更高深的技巧及社交能力囉..

不過就是寫程式嘛, 保持學習的心, 高度的興趣, 自然就能做得好..(應該各行業也都是這樣吧. XD)