標籤: graph

用 Facebook 的網頁/網站很多, 應該是已經過了大流行的階段, 但是使用 Facebook 的地方還是很多, 如何利用程式將公開性的 Facebook 資料找查出來, 有方便好用的工具可供應用, 就是使用 FQL 查詢. 這裡介紹一般常用在網頁上留言的資料, Comment Plugin, 查找留言資訊.

先來看這篇: https://developers.facebook.com/docs/reference/fql/comment

這篇介紹 FQL 的 comment 資料查找方式, 我們以這個網頁作為例子:
http://sample.diary.tw/18/maps.htm

這裡裝了 Facebook 的 comment plugin, 那我們要查找該頁中 comment 的資料要怎麼查找呢? 首先要先找到該 comment 的 object_id, 該 id 可以利用這頁來找:
https://developers.facebook.com/tools/debug

將上面的 http://sample.diary.tw/18/maps.htm 輸入後, 按下[除錯]鈕, 在最下面的網址可以得到該 comment 的 object_id 為: 10150561101545602, 這個就是在 FQL 中, 查詢 comment 的 object_id. (在 Facebook 中, 會給定的各 object id)

再來就要下 FQL 查找資料了, 語法如下:

SELECT id, text, time, fromid FROM comment WHERE object_id='10150561101545602'

問題是從哪裡下呢? 從這裡 Graph API Explorer:
https://developers.facebook.com/tools/explorer
(若無法使用, 會引導登入 Facebook, 使用 Graph API Explorer需要登入 Facebook)

再將中間原來預設為 Graph API 的功能切到 FQL Query, 接下來把上面的查詢指令輸入, 就會得到目前的留言資料, 以 json 的方式來顯示.
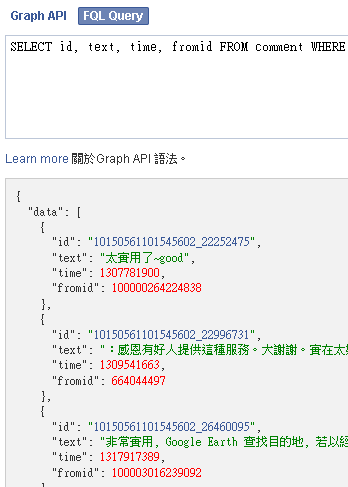接下來的使用, 相信大家就應該容易多了, 就是解析 json 把資料取出來即可.

那如何使用呢? 在程式中如何呼叫這個查詢, 而不是用 Graph API Explorer, 有沒有看到瀏覽器上方的 url 已經變了, 如下:
https://developers.facebook.com/tools/explorer?fql=SELECT%20id%2C%20text%2C%20time%2C%20fromid%20FROM%20comment%20WHERE%20object_id%3D%2710150561101545602%27
也就是說, 其實就是把查詢放到 url 中的 q 參數即可, 但使用上, 前面的 Graph API Explorer 得改成如下:
https://graph.facebook.com/fql?q=SELECT%20id%2C%20text%2C%20time%2C%20fromid%20FROM%20comment%20WHERE%20object_id%3D%2710150561101545602%27
使用 Graph FQL 查詢即可, 這是不用登入就可以使用的, 也就是說, 在程式中只需要透過 webget 等方法, 就可以取得到內容.

應該會有人問, 這個查詢結果, 其中的 text 是留言沒錯, 但沒有人名, 大頭圖, 那怎麼辦, 很簡單啊, 就再回 FQL 查詢就可以了, 不過若是有 100篇留言就要查 100次耶, 或是 smart 一點, 100篇留言, 共 30 個人在留, 那也需要做 30次的 user 查詢, 怎麼想都很難處理, 所以接下來要介紹的是多重查詢.

多重查詢, 有點像是 SQL 中的子查詢, 在面對這種 FQL 查詢時, 可以利用的技巧, 我們將查詢改一下, 改為如下:

{
"comments": "SELECT id, text, time, fromid FROM comment WHERE object_id='10150561101545602'",
"commenters": "SELECT uid, name, pic_square FROM user WHERE uid IN (SELECT fromid FROM #comments)"
}

對, 正如你看到的, 使用一個 #comments 代替前一個查詢結果, 並代入下一個查詢, 利用 json 格式, 將多重查詢放到 FQL 中, 就可以一次查詢把留言和人帶回來, 忘了說, user FQL 參考資料在這裡:
https://developers.facebook.com/docs/reference/fql/user

第二個查詢中的 uid, name, pic_square 就是常用的使用者代碼, 名稱, 大頭圖資訊.
查詢回傳結果就會有兩個 fql_resulte_set, 分別就是 comments, commenters, 如下: